PSC 128/NPB 163 - Information processing models
Lab #2 - Linear neuron models
(due Friday, Jan. 16)
1. Model fitting. This problem is designed to show the perils
of over-fitting data, similar to what was discussed in class. We provide
a simulated dataset of "characteristic frequency" (cf) and "bandwidth" (bw)
for 200 auditory cells. With these data, "cf" is considered the independent
variable (i.e., the x-axis) and "bw" the dependent variable (y-axis). You
can get this data set, hw1.mat, from the class homepage. You should plot
the data first as individual data points. Here are some commands to get
started:
>> load hw1.mat
>> whos
>> plot(cf,bw,'.')
(a) The variables cfsub and bwsub contain a subset of seven points extracted
from the total dataset. Create a linear fit to this subsample of the data
using the matlab routine polyfit.
(b) Now create a 5th-order polynomial fit to the subsample.
(c) Plot both fits, shown as solid lines, along with the subsample, shown
as individual data points, on the same plot. Which of these fits the subsample
better?
(d) Now plot both of your function fits from (a) and (b) along with the
entire dataset. Which of these fits the entire data better? What's
going on?
2. Vectors. Given the two-dimensional vector 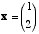 .
.
(a) Create a vector y that is orthogonal to x. Show
both x and y together on the same plot, using Matlab. Use different line
styles for x and y and use 'legend' to denote which is
which.
(b) Create a vector z that is not orthogonal to x
and plot both x and z in Matlab. Compute the angle between
these vectors using the inner product and inverse cosine (acos).
3. Linear neuron. Let’s say we have a linear neuron with two
inputs 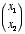 whose corresponding weights are
whose corresponding weights are 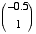 . Plot the weight vector within the 2D space
. Plot the weight vector within the 2D space 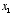 ,
,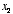 and shade the portion of the input space for which the neuron would have
a positive output value. (It may be easier to just do this by hand rather
than in Matlab.)
and shade the portion of the input space for which the neuron would have
a positive output value. (It may be easier to just do this by hand rather
than in Matlab.)
4. Receptive field models. Load the three receptive fields DOG.mat, Gaborh.mat, and Gaborv.mat (corresponding to three different neurons), in
addition to the edge images (edges.mat) and the
Einstein image (einstein.mat)
from the class homepage.
(a) Plot the three different receptive fields side by side within the same
figure using imagesc and subplot so you can see what they look like. Use
the scaling option for imagesc to make sure that the grayscale for each is
equivalent - i.e., so they are directly comparable.
(b) Show what each of the edge images looks like in the same manner - i.e.,
by showing them side by side in the same figure using subplot. You should
see that they are just edges at different positions and orientations.
(c) Now, for each of your neurons, compute the inner product between its
receptive field and each of the edge images. Plot your results for each
neuron as a bar plot, with the position of the edge on the x-axis of each
barplot.
(d) Finally, for each neuron, show what it would look like to have an entire
array of these neurons processing the Einstein image. You can do this by
typing
pim=conv2(einstein,DOG,’same’);
where pim is your processed image. The function conv2 simply takes the
array in the second argument, and computes the inner product between it and
the array in the first argument at different positions within the array.
(This procedure of repeatedly computing inner products at different positions
is called a 'convolution,' which we'll discuss next week.)
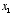 ,
,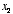 and shade the portion of the input space for which the neuron would have
a positive output value. (It may be easier to just do this by hand rather
than in Matlab.)
and shade the portion of the input space for which the neuron would have
a positive output value. (It may be easier to just do this by hand rather
than in Matlab.)